- the probability that it will rain in Cardiff tomorrow is 0.8
- the probability that there are Sea Gulls on Roath Park lake given that it will rain tomorrow is 0.1
- the probability that there are Sea Gulls on Roath Park lake given that it will NOT rain tomorrow is 0.05
What is the probability that it will rain tomorrow given that there a Sea Gulls on Roath Park lake?
- What are my initial disbelief and certainty factors that it will rain?
- What are the new estimates of belief, disbelief and certainty factors based on both observations.
I then catch a weather forecast states that there 50am. What is my belief, disbelief and certainty factors based on my observations and the weather forecast?

- The probability that following an observation of fever that Flu, Cold or Pneumonia cause it is 0.6.
- The probability of fever caused by Allergy, Flu or Cold is 0.8.
- Use the Dempster combination rule to compute beliefs for further subsets derived from the above.
- We now discover that probability of allergy is 0.8. Combine this information to compute the beliefs for all possible outcome of set intersections.
- patient has spots
- patient has measles
- patient has a fever
- patient has been inoculated against measles
- patient has been bitten by an insect recently
- patient has an allergy to insect bites.
- Construct a set of MYCIN rules that could diagnose both measles and
allergy. (You may assume any probabilities you deem reasonable).
Show how you would use these rules to reach the belief that the patient has an insect bite allergy.
- Consider representing the proposition in Dempster-Shafer theory. How
would you define
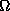 and the set of M belief functions to describe
dependencies between the sources of evidence and elements of
and the set of M belief functions to describe
dependencies between the sources of evidence and elements of 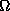 .
.
Show how you reach the belief that the patient has an insect bite allergy.
- Create a network that that defines causal connections between nodes.
- Modify the above network to become a Bayesian network by constructing an appropriate probability matrix.
Assume that two pieces of uncertain data have been gathered today:
- The temperature is below freezing.
- The barometric pressure is falling so a storm is likely.
Let Table 1 represent the probabilities of a storm and
a freeze occurring over the Dempster-Shafer power set ![]() where
where ![]() distributes mass for freezing probabilities and
distributes mass for freezing probabilities and
![]() similarly for storm statistics.
similarly for storm statistics.

Table: Cardiff Weather forecast
- Let
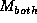 represent a function that distributes mass for both storm
and freezing evidence. Assuming that
represent a function that distributes mass for both storm
and freezing evidence. Assuming that 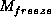 and
and 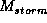 represent
items of evidence that are independent of each other complete the above table
using Dempster's rule of combination.
represent
items of evidence that are independent of each other complete the above table
using Dempster's rule of combination.
- Calculate the degrees of belief in the proposition that it will both snow and rain tomorrow based on all the combined evidence. Compare this result to that if only freeze or storm information is present.
- Without resorting to computation What is the degree of belief in
that it will either snow, rain or remain dry under any form of evidence
presented above (
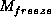 ,
, 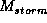 or
or 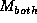 ).
).
- What is the belief that it will be snowing and / or dry tomorrow based
upon
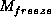 ,
, 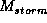 and
and 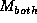
- What is the doubt that there will be snow tomorrow given that it is
freezing and the pressure is falling. The Doubt of an event A is define a
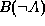 i.e. the belief in all evidence that contradicts A.
i.e. the belief in all evidence that contradicts A.
- What is the plausibilitythat there will be snow tomorrow given that it is freezing and the pressure is falling.
There is some evidence that provides equal support for the murderer being male or female. There is also evidence that Peter was has an alibi for the time of the killing.
- Combine the information above and represent it in the Dempster-Shafer formalism.
- Calculate the Belief and Plausibility for each suspect.
- I saw my cat in the living room 3 hours ago.
- Two hours ago my door blew open.
- Three quarters of the time my door blows open my cat runs outside through the door.
- On hour ago I thought I heard a cat-noise in my living. Assume I was half certain.
- In any one hour period the probability that the cat will leave the room is 0.2. There is also a 0.2 probability that he may enter the room.
What is the Certainty that the cat is in my living room?
- Use Dempster-Shafer theory to answer this.
- Use Bayesian networks to answer this.
- If the following probabilities are assigned to the respective events what
is the probability that my car will be sent to the garage?. Also show how
this information is illustrated in the Bayesian network.
- My car has a 60
- If my car won't start the probability of the battery being flat is 0.3 and the starting motor being defective is 0.1.
- If the headlights do not work then the probability of the battery being flat is 0.7.
- The probability of both battery and headlights being defective is 0.05.
- How could add the following information to the network:
- If the car wont start and there is crunching noise coming from the engine then the starting motor is defective.
- If the headlights do not work then the lights themselves maybe defective.
- There may be another reason why my car will not start.
- I ask two garages for estimates for the repair work and I choose the cheapest.
- Choosing a menu for a dinner party.
- Planning a holiday.
- Selecting final year computer science options based on second and first year prerequisites.