Here we will consider some extensions to Semantic nets that overcome a few problems (see Exercises) or extend their expression of knowledge.
Partitioned Networks Partitioned Semantic Networks allow for:
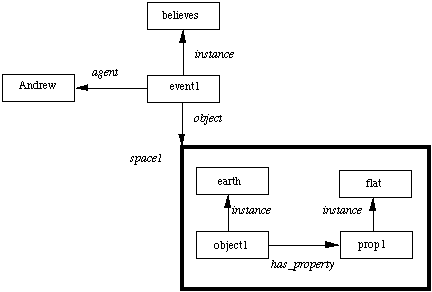
Consider the following:
Andrew believes that the earth is flat.
We can encode the proposition the earth is flat in a space and
within it have nodes and arcs the represent the fact
(Fig. 15).
We can the have nodes and arcs to link this
space the the rest of the network to represent Andrew's belief.

Fig. 12 Partitioned network
Now consider the quantified expression: Every parent loves their child To represent this we:
Here we have to construct two spaces one for each x,y.
NOTE: We can
express ![]() variables as existentially qualified variables and
express the event of love having an agent p and receiver b
for every parent p which could simplify the network (See Exercises).
variables as existentially qualified variables and
express the event of love having an agent p and receiver b
for every parent p which could simplify the network (See Exercises).
Also If we change the sentence to Every parent loves child then the node of the object being acted on (the child) lies outside the form of the general statement. Thus it is not viewed as an existentially qualified variable whose value may depend on the agent. (See Exercises and Rich and Knight book for examples of this) So we could construct a partitioned network as in Fig. 16
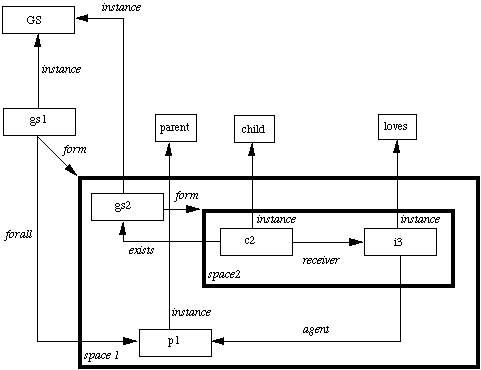
Fig. 12 ![]() Partitioned network
Partitioned network