Considering a continuous function f(x) of a single variable x representing distance.
The Fourier transform of that function is denoted F(u), where u represents spatial frequency is defined by
| (1) |
Note: In general F(u) will be a complex quantity even though the original data is purely real.
The meaning of this is that not only is the magnitude of each frequency present important, but that its phase relationship is too.
The inverse Fourier transform for regenerating f(x) from F(u) is given by
| (2) |
Let's see how we compute a Fourier Transform: consider a particular function f(x) defined as
| (3) |
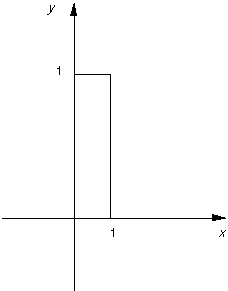
A top hat function
So its Fourier transform is:
In this case F(u) is purely real, which is a consequence of the original data being symmetric in x and -x. A graph of F(u) is shown in Fig. 7.7. This function is often referred to as the Sinc function.
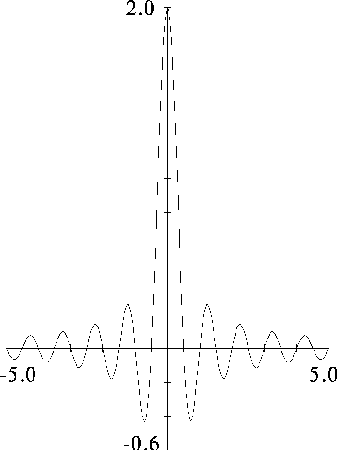
Fourier transform of a top hat function