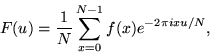
Images and Digital Audio are digitised !!
Thus, we need a discrete formulation of the Fourier transform, which takes such regularly spaced data values, and returns the value of the Fourier transform for a set of values in frequency space which are equally spaced.
This is done quite naturally by replacing the integral by a summation, to give the discrete Fourier transform or DFT for short.
In 1D it is convenient now to assume that x goes up in steps of 1, and that there are N samples, at values of x from 0 to N-1.
So the DFT takes the form
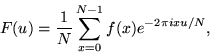 |
(6) |
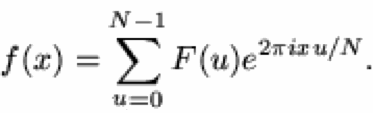 |
(7) |
NOTE: Minor changes from the continuous case are a factor of 1/N in the exponential terms, and also the factor 1/N in front of the forward transform which does not appear in the inverse transform.
The 2D DFT works is similar. So for an ![]() grid in
x and y we have
grid in
x and y we have
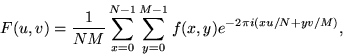 |
(8) |
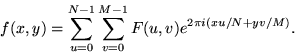 |
(9) |
Often N=M, and it is then it is more convenient to redefine F(u,v) by multiplying it by a factor of N, so that the forward and inverse transforms are more symmetrical:
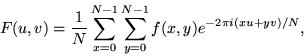 |
(10) |
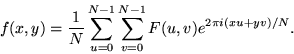 |
(11) |