Publications

Diffusion Pruning for Rapidly and Robustly Selecting Global Correspondences using Local Isometry
ACM Transactions on Graphics, vol. 33(1), Article No. 4, pp. 1-17.
Gary K.L. Tam, Ralph R. Martin, Paul L. Rosin and Yu-Kun Lai

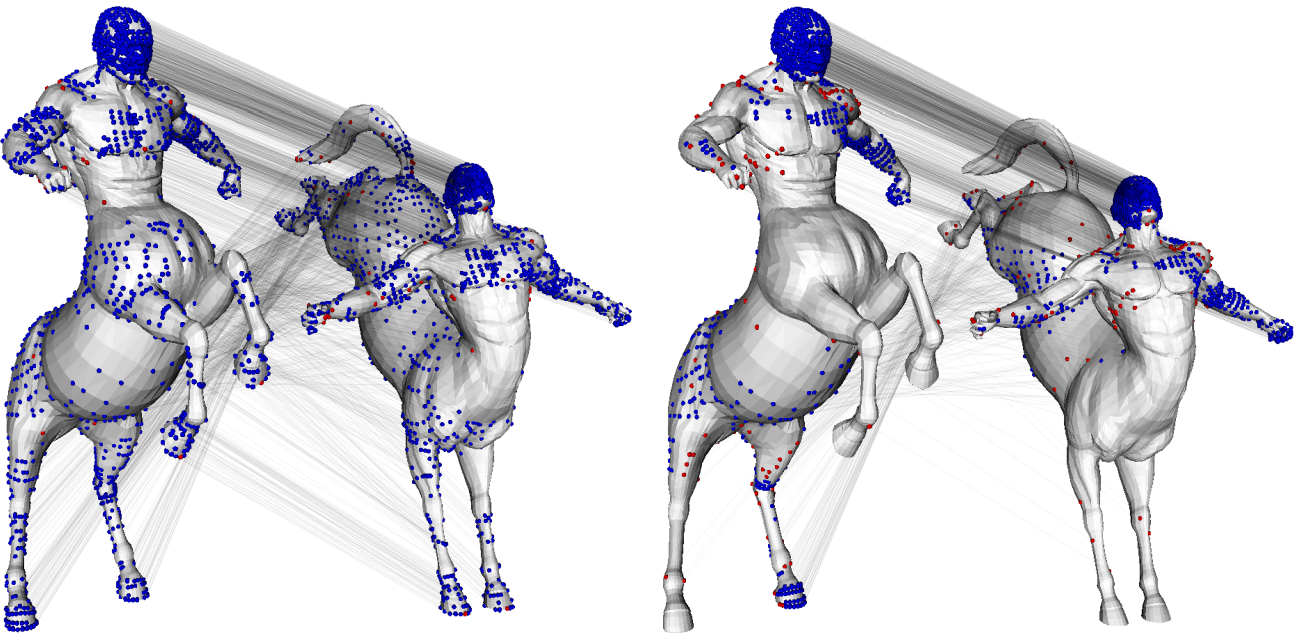
Finding correspondences between two surfaces is a fundamental operation in various applications in computer graphics and related fields. Candidate correspondences can be found by matching local signatures, but as they only consider local geometry, many are globally inconsistent. We provide a novel algorithm to prune a set of candidate correspondences to those most likely to be globally consistent. Our approach can handle articulated surfaces, and ones related by a deformation which is globally non-isometric, provided that the deformation is locally approximately isometric. Our approach uses an efficient diffusion framework, and only requires geodesic distance calculations in small neighbourhoods, unlike many existing techniques which require computation of global geodesic distances. We demonstrate that, for typical examples, our approach provides significant improvements in accuracy, yet also reduces time and memory costs by a factor of several hundred compared to existing pruning techniques. Our method is furthermore insensitive to holes, unlike many other methods.

An Efficient Approach to Correspondences between Multiple Non-Rigid Parts
Computer Graphics Forum (SGP 2014), vol. 33(5), pp. 137-146.
Gary K.L. Tam, Ralph R. Martin, Paul L. Rosin and Yu-Kun Lai

Identifying multiple deformable parts on meshes and establishing dense correspondences between them are tasks of fundamental importance to computer graphics, with applications to e.g. geometric edit propagation and texture transfer. Much research has considered establishing correspondences between non-rigid surfaces, but little work can both identify similar multiple deformable parts and handle partial shape correspondences. This paper addresses two related problems, treating them as a whole: (i) identifying similar deformable parts on a mesh, related by a non-rigid transformation to a given query part, and (ii) establishing dense point correspondences automatically between such parts. We show that simple and efficient techniques can be developed if we make the assumption that these parts locally undergo isometric deformation. Our insight is that similar deformable parts are suggested by large clusters of point correspondences that are isometrically consistent. Once such parts are identified, dense point correspondences can be obtained by an iterative propagation process. Our techniques are applicable to models with arbitrary topology. Various examples demonstrate the effectiveness of our techniques.

Lp Shape Deformation
Science China Information Sciences, vol. 55(5), pp. 983-993, 2012.
Lin Gao, Guo-Xin Zhang and Yu-Kun Lai

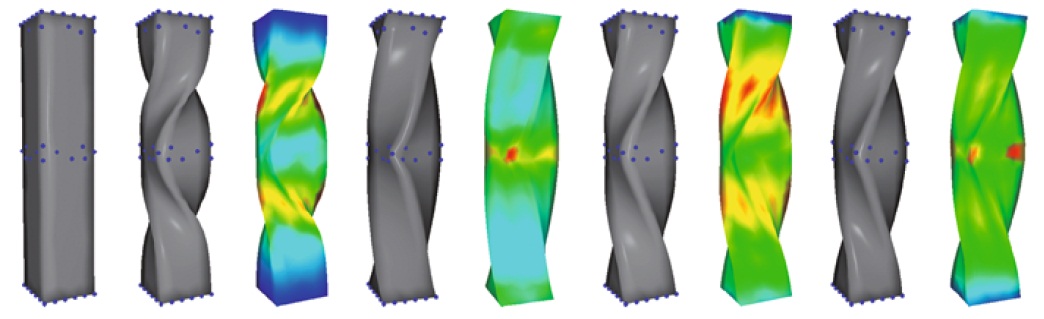
Shape deformation is a fundamental tool in geometric modeling. Existing methods consider preserving local details by minimizing some energy functional measuring local distortions in the L2 norm. This strategy distributes distortions quite uniformly to all the vertices and penalizes outliers. However, there is no unique answer for a natural deformation as it depends on the nature of the objects. Inspired by recent sparse signal reconstruction work with non L2 norm, we introduce general Lp norms to shape deformation; the positive parameter p provides the user with a flexible control over the distribution of unavoidable distortions. Compared with the traditional L2 norm, using smaller p, distortions tend to be distributed to a sparse set of vertices, typically in feature regions, thus making most areas less distorted and structures better preserved. On the other hand, using larger p tends to distribute distortions more evenly across the whole model. This flexibility is often desirable as it mimics objects made up with different materials. By specifying varying p over the shape, more flexible control can be achieved. We demonstrate the effectiveness of the proposed algorithm with various examples.

Vertex Location Optimisation for Improved Remeshing
Graphical Models, vol. 74(4), pp. 233-243, 2012.
Yu-Kun Lai and Ralph R. Martin

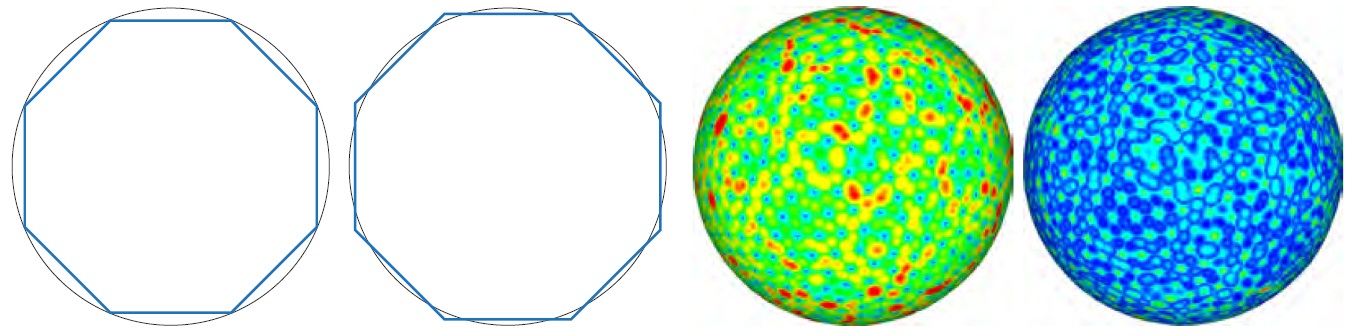
Remeshing aims to produce a more regular mesh from a given input mesh, while representing the original geometry as accurately as possible. Many existing remeshing methods focus on where to place new mesh vertices; these samples are placed exactly on the input mesh. However, considering the output mesh as a piecewise linear approximation of some geometry, this simple scheme leads to significant systematic error in nonplanar regions. Here, we use parameterised meshes and the recent mathematical development of orthogonal approximation using Sobolev-type inner products to develop a novel sampling scheme which allows vertices to lie in space near the input surface, rather than exactly on it. The algorithm requires little extra computational effort and can be readily incorporated into many remeshing approaches. Experimental results show that on average, approximation error can be reduced by 40% with the same number of vertices. A similar technique can also be applied to surface normals to provide more accurate rendering results with the same number of vertices.